The Fokker-Planck equation has a stationary solution, for a biased periodic potential:

A Brownian ratchet occurs when the potential is asymmetric. A particularly nice example is the sawtooth potential, in which the above equation gives:

for the first site.

We find three regimes:

The drift velocity is:

which plotted looks like:

This shows an asymmetry between the positive and negative force regions, similar to that shown in the current-voltage curve of a diode:

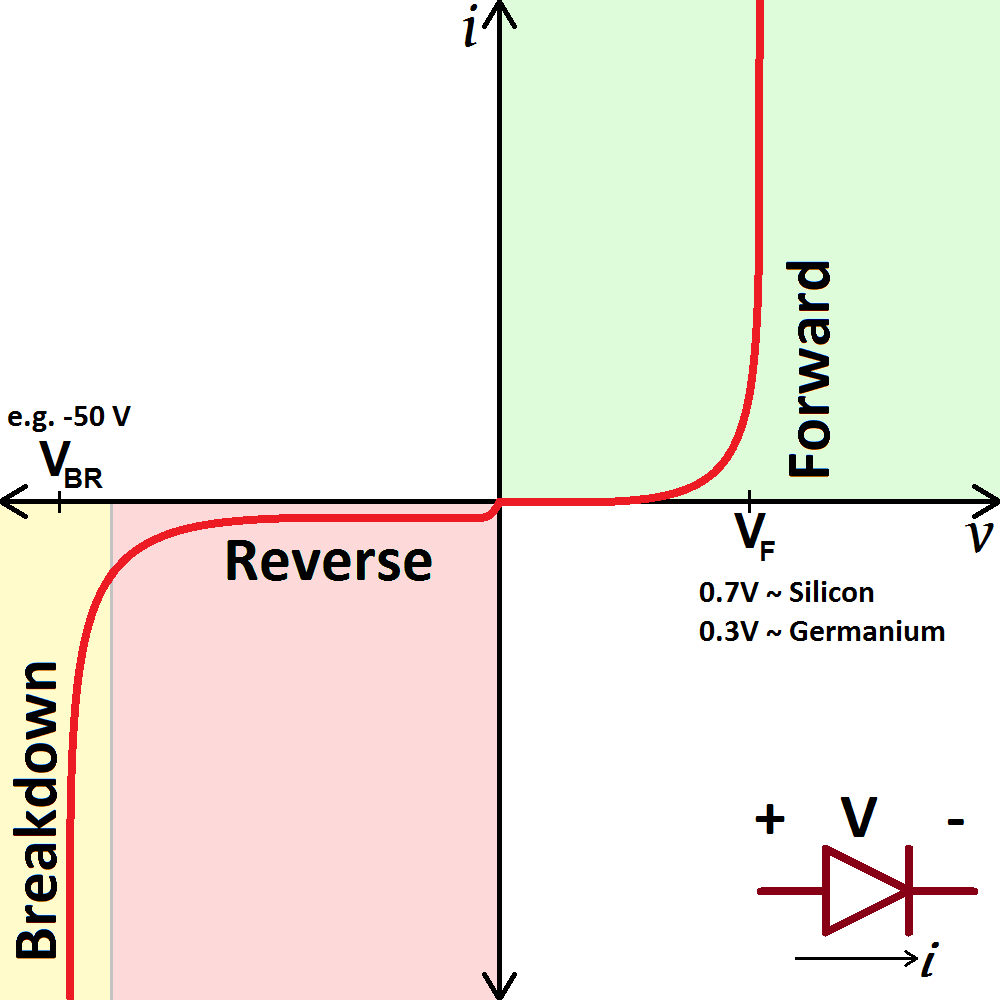
In fact ratchets and diodes are very analogous, and ratchets, including Brownian ratchets can be thought of as mechanical diodes. In fact, the famous Feynman Brownian ratchet paradox was formulated by Brillouin in terms of a diode rectifier (Brillouin paradox)

This rectification in Brownian ratchets can be used as a basis for fluctuation-driven transport, which is a proposed mechanism for molecular motors. See here

An example of this is in the tilting ratchet, in which the bias $F$ used above, oscillates.

Flashing ratchet

Another example of a Brownian ratchet is when the potential $U(x)$ itself oscillates (fluctuations between a low and a high potential). A special case has the potential turning stochastically between two states, this is known as the flashing ratchet, if one of the two states has no potential, this is called the on-off ratchet.

A way to solve for the probability in the stochastically flashing ratchet is to add a new label to the probability representing one of the two states of the potential landscape, call them $+$ and $-$. Then we get a Fokker-Planck/Master equation for our continuous (space labelled by $\vec{x}$) and discrete configuration space:

One can the workout the evolution equation for the total probability of being at position $\vec{x}$, and it turns out to have the form of a Fokker-Planck equation with an effective potential.