Diffusiophoresis is the process by which particles move trough a chemical concentration gradient, due to an attractive or repulsive interaction between the particle and the chemical compound. It is a kind of phoretic mechanism of colloids.

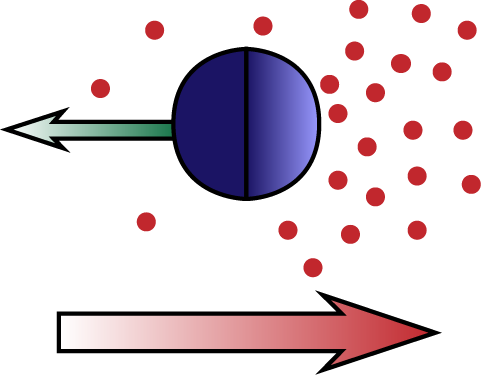
Essentially, the surface of the particle, due to Intermolecular forces (or other entropic forces), can be attracted, or repelled to the solvent molecules. If there is a gradient in the concentration of these, they can exert a net force on the particle causing it to gain a certain velocity (and the particle will exert a force on the fluid, causing it to slip over its surface).

In Self-diffusiophoresis (a kind of self-propulsion), the particle itself produces the compound it interacts with.

http://pubs.acs.org/doi/abs/10.1021/la00050a035

https://en.wikipedia.org/wiki/Diffusiophoresis

http://link.springer.com/referenceworkentry/10.1007/978-3-642-27758-0_328-5#page-1

Particle motion driven by solute gradients with application to autonomous motion: continuum and colloidal perspectives

Theory

When the thickness of the interfacial layer is thin compared to the object, the resulting flow is most conveniently described by an effective slip velocity of the liquid past the solid at position $r_s$ on the surface, proportional to the local gradient of $c$. See a simple derivation below (from Colloid Transport by Interfacial Forces).

_{(I think they are missing a d on the bottom in (9))}

See derivation in the black notebook. Note that at the end you need to use the trick of changing order of integration, as done in Derjaguin's original paper (on page 7).

The general tensorial equation is:

$\mathbf{v}_s(\mathbf{r}_s) = \mu (\mathbf{r}_s)(\mathbf{I}-\mathbf{n}\mathbf{n}) \cdot \nabla c (\mathbf{r}_s)$

$\mu (\mathbf{r}_s)$ is the local surface phoretic mobility, which depends on the particular interaction between the particle and the solven molecules (through the integral in (9)).

Then using the reciprocal theorem (of Low Reynolds number flows), one can find the velocity of the particle, knowing the slip velocity of the solvent around it. In a given basis, the drift velocity of the colloid, $\mathbf{V}$, is then:

$\mathbf{V}\cdot \hat{\mathbf{f}}_i = - \int \int_S d \mathbf{r}_s \mathbf{n} \cdot \mathbf{\sigma}_i \cdot \mathbf{v}_i$

where $\mathbf{\sigma}_i$ is the hydrodynamic stress tensor at the surface $S$ of an object of the same shape dragged by an applied unit force, $\hat{\mathbf{f}}_i = \hat{\mathbf{e}}_i$ exactly equal to $\hat{\mathbf{e}}_i$, in the absence of slip.

In the case of spherical particles, the drift velocity turns out to be simply:

$\mathbf{V} = -\frac{1}{4\pi} \int \mathbf{v}_s d\Omega$

For uniform motility, $\mathbf{v}_s = \mu \nabla_{||}c$, and so

$\mathbf{V} = -\mu \nabla_{||}c$

This simple equation for the velocity is appropriate for the Active colloids used in studying the Self-assembly of active colloids.

See Hydrodynamic slip

In the derivation of equation (9) they assumed that $\Phi$ doesn't depend on $x$. Is this the reason why a particle without a gradient in $c$, even if it has a gradient in its phoretic mobility is predicted to have $0$ drift velocity? Would you get a non-zero velocity if you took dependence on $x$ of $\Phi$ into account?

See Diffusiophoresis caused by gradients of strongly adsorbing solutes

Giant Amplification of Interfacially Driven Transport by Hydrodynamic Slip: Diffusio-Osmosis and Beyond

Diffusiophoresis: Migration of Colloidal Particles in Gradients of Solute Concentration

Kinetic Phenomena in the boundary layers of liquids 1. the capillary osmosis